In Support of Inflation

Alejandro Gangui

What created the initial inhomogeneities in the Universe that resulted in galaxies, clusters of galaxies and other large-scale structures? This problem continues to puzzle cosmologists. But whatever the mechanism, it must have left its signature in the cosmic microwave background (CMB) radiation [1]. The CMB is a relic of the big bang, a cold bath of light just a few degrees above absolute zero that pervades the entire the Universe. Released when matter began to become structured, the CMB is our earliest ``snapshot'' of the Universe. Variations (or anisotropies) in its effective temperature tell us about the size and strength of the initial seeds in the primordial plasma, those clouds of gas that clumped together under gravitational attraction and led to the birth of galaxies. Recent CMB experiments suggest that these fundamental seeds could have resulted from tiny primordial quantum fluctuations generated in the early Universe during a period of rapid (faster than light) expansion called inflation.

Early on, when the Universe was small and very hot, the free electron density was so high that photons could not propagate freely without being scattered by electrons. Ionized matter, electrons and radiation formed a single fluid, with the inertia provided by the baryons and the radiation pressure given by the photons. And this fluid supported sound waves. In fact, the gravitational clumping of the effective mass in the perturbations was resisted by the restoring radiation pressure, resulting in gravity-driven acoustic oscillations in both fluid density and local velocity.

As the Universe expanded and ambient temperatures decreased, high-energy collisions became less and less frequent. Very energetic photons were not statistically significant to destroy the increasing number of neutral particles (mostly hydrogen) that began to combine. Cosmologist refer to this period as recombination. Soon afterwards the CMB was released free, making its last scattering upon matter. This is a remarkable event in the history of the Universe, because it is the very moment when it passed from being opaque to being transparent to electromagnetic radiation.

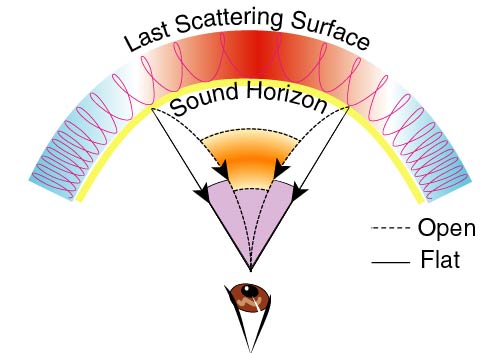Features in the radiation pattern at this time depend on the maximum distance a sound wave could have traveled since the Big Bang - the sound horizon. Cosmological models relate this distance to the angle $\theta$ it subtends on the sky today through the angular-diameter distance relation [2]. This relation depends on the various unknown cosmological parameters, most importantly the total energy density in the Universe. But according to Einstein's general relativity, energy implies curvature. Hence, the curvature of the Universe affects the angle $\theta$ subtended today by the sound horizon at recombination (see the first figure). For a Universe devoid of spatial curvature (a flat or Euclidean geometry) models predict $\theta\approx 1^\circ$. Thus, if the Universe were flat, at an angular scale of precisely $1^\circ$ we would expect to detect some characteristic feature in the CMB, the ``fingerprint'' of recombination.

How can this feature be detected? One convenient way of comparing theoretical model predictions with the result of observations is by means of the functions $C_\ell$, the CMB angular power spectrum of the anisotropies. The microwave sky is expanded into a set of functions labeled by the multipole index $\ell$. The correspondence is such that the $\ell$th multipole samples angular scales of order $\theta\sim 180^\circ/\ell$. Hence, $C_\ell$ gives us the typical strength of the temperature perturbations on that angular scale. A characteristic feature is given by the presence of peaks in the $\ell(\ell+1)C_\ell$ versus $\ell$ plot. The first acoustic peak is located at the multipole corresponding to the scale of the sound horizon at recombination, when the plasma underwent its first oscillation; it corresponds to a compression mode of the oscillating plasma.

Last year, the BOOMERanG collaboration announced results from the Antarctic long duration balloon flight mission of 1998 (B98). They found the first peak located at $\ell\sim 200$, at the right position for a flat Universe [3,4]. Only weeks later, the results from another balloon experiment, MAXIMA, were made available on the internet [5,6]. MAXIMA produced high-resolution maps of a 100 square-degree patch of the northern sky and went beyond B98 in exploring multipoles from $\ell\simeq 36$ to 785, the largest range reported to date with a single experiment.

Recently, a joint analysis of the COBE/DMR [7], B98 and MAXIMA data sets was published [8]. The COBE data provide information at low $\ell$, necessary for normalization purposes. After correcting for calibration uncertainties, the B98 and MAXIMA data were quite consistent. The experiments used different observation strategies and produced independent power spectra from regions of the sky roughly $90^\circ$ apart and on opposite sides of the galactic plane. Their consistency gives confidence in the results (see the second figure).

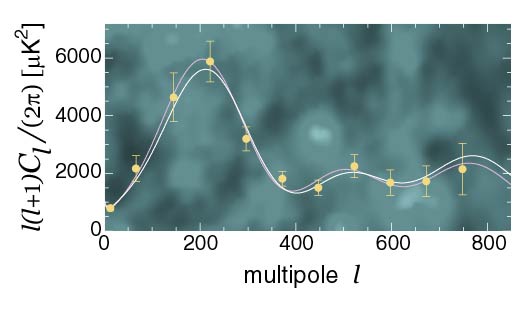The presence of a localized and narrow ( $\Delta\ell/\ell \sim 1$) peak at $\ell\sim 200$ is in agreement with a flat Universe and favors an inflationary model with initial adiabatic perturbations (where fluctuations in each species are correlated). In the absence of a possible later period of reionization, which could erase partly or even completely the acoustic peaks, the physics of recombination predicts the existence of other peaks; the second one corresponds to a rarefaction mode and its characteristic scale is half that of the first peak. In the actual data we can see that following the first peak there is a hint of a second one at $\ell\sim 500$, but nothing conclusive can be said yet.

Alternative models cannot reproduce these observations. Cosmic topological defects in their simplest versions do not predict the existence of this oscillation pattern. Topological defects, such as cosmic strings and textures, which are concentrations of primordial energy issued from early cosmological phase transitions, can produce structure in the Universe, but cannot fit the present data [9,10]. The complicated nonlinear evolution of the defect network continuously perturbs the radiation background all along the photon's journey in an incoherent fashion, leaving as its sole characteristic signature a broad hump and virtually no acoustic peaks [11]. Recent computer simulations with a cosmic string model [12] have failed to generate the level of CMB variations observed by B98 and MAXIMA on scales below $1^\circ$.

The accurate locations and amplitudes of the expected secondary peaks will allow the determination of many fundamental cosmological parameters, such as a possible cosmological constant $\Lambda$ or other forms of dark energy, such as quintessence [13]. Full analysis of the B98 and MAXIMA data sets will provide further insights, but conclusive results will require inclusion of CMB polarization data [14] and full sky coverage from the forthcoming satellite-based mission MAP [15]. Other astrophysical input, such as supernovae and large scale structure data, in combination with the CMB, has proven very successful for removing degeneracies in the determination of fundamental parameters and will be even more important in the future.

The increasing precision of today's detectors demands theoretical modeling to be highly accurate. The CMB contains a wealth of information on cosmology, and future experiments will test our models of structure formation to the limit.

References and Notes

1. D. Scott et al., Science 268, 829 (1995) [ADS].
2. S. Weinberg, preprint available at arXiv.org/abs/astro-ph/0006276.
3. P. de Bernardis et al., Nature 404, 955 (2000) [ADS].
4. C. Seife, Science 288, 595 (2000).
5. A. Balbi et al., Astrophys. J. 545, L1 (2000) [ADS].
6. S. Hanany et al., Astrophys. J. 545, L5 (2000) [ADS].
7. C. Bennett et al., Astrophys. J. 464, L1 (1996) [ADS].
8. A. Jaffe et al., Phys. Rev. Lett., in press.
9. R. Durrer, A. Gangui, M. Sakellariadou, Phys. Rev. Lett. 76, 579 (1996) [APS]; preprint available at arXiv.org/abs/astro-ph/astro-ph/9507035.
10. U.-L. Pen, U. Seljak, N. Turok, Phys. Rev. Lett. 79, 1611 (1997) [APS].
11. J. Magueijo et al., Phys. Rev. Lett. 76, 2617 (1996) [APS].
12. L. Pogosian, preprint available at arXiv.org/abs/astro-ph/0009307
13. N. Bahcall et al., Science 284, 1481 (1999).
14. M. Hedman et al., Astrophys. J., in press.
15. See the Microwave Anisotropy Probe home page at map.gsfc.nasa.gov.
16. The author is supported by Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) and the University of Buenos Aires (Argentina).

Some citing www pages:
* Research Preprint Highlights - February 2001 : Astrophysics (14 chosen from 506 preprints) .
* The Net Advance of Physics: INFLATION (Cosmology)  . Or here .
* [sprechen Sie deutsch? - read the news on the Sternwarte Neumarkt then...] - [also here, in Astronomie-News] .


 

back to IAFE home page

Back

back to GRQTG home page

The URL of this page is http://www.iafe.uba.ar/relatividad/gangui/maxima_science/ .
Edited by Alejandro Gangui