What created the initial inhomogeneities in the Universe that resulted in galaxies, clusters of galaxies and other large-scale structures? This problem continues to puzzle cosmologists. But whatever the mechanism, it must have left its signature in the cosmic microwave background (CMB) radiation [1]. The CMB is a relic of the big bang, a cold bath of light just a few degrees above absolute zero that pervades the entire the Universe. Released when matter began to become structured, the CMB is our earliest ``snapshot'' of the Universe. Variations (or anisotropies) in its effective temperature tell us about the size and strength of the initial seeds in the primordial plasma, those clouds of gas that clumped together under gravitational attraction and led to the birth of galaxies. Recent CMB experiments suggest that these fundamental seeds could have resulted from tiny primordial quantum fluctuations generated in the early Universe during a period of rapid (faster than light) expansion called inflation.
Early on, when the Universe was small and very hot, the free electron density was so high that photons could not propagate freely without being scattered by electrons. Ionized matter, electrons and radiation formed a single fluid, with the inertia provided by the baryons and the radiation pressure given by the photons. And this fluid supported sound waves. In fact, the gravitational clumping of the effective mass in the perturbations was resisted by the restoring radiation pressure, resulting in gravity-driven acoustic oscillations in both fluid density and local velocity.
As the Universe expanded and ambient temperatures decreased, high-energy collisions became less and less frequent. Very energetic photons were not statistically significant to destroy the increasing number of neutral particles (mostly hydrogen) that began to combine. Cosmologist refer to this period as recombination. Soon afterwards the CMB was released free, making its last scattering upon matter. This is a remarkable event in the history of the Universe, because it is the very moment when it passed from being opaque to being transparent to electromagnetic radiation.
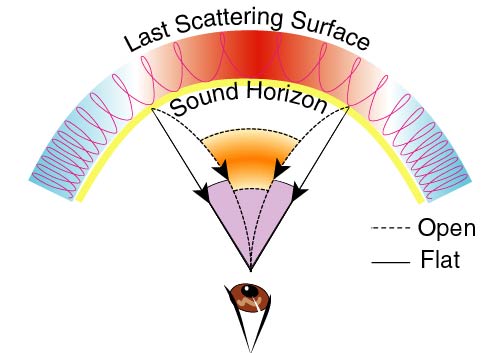 |
Features in the radiation pattern at this time depend on the maximum
distance a sound wave could have traveled since the Big Bang - the
sound horizon. Cosmological models relate this distance to the
angle ![]() it subtends on the sky today through the
angular-diameter distance relation [2]. This relation
depends on the various unknown cosmological parameters, most
importantly the total energy density in the Universe. But according to
Einstein's general relativity, energy implies curvature. Hence, the
curvature of the Universe affects the angle
it subtends on the sky today through the
angular-diameter distance relation [2]. This relation
depends on the various unknown cosmological parameters, most
importantly the total energy density in the Universe. But according to
Einstein's general relativity, energy implies curvature. Hence, the
curvature of the Universe affects the angle ![]() subtended today
by the sound horizon at recombination (see the first figure). For a
Universe devoid of spatial curvature (a flat or Euclidean geometry)
models predict
subtended today
by the sound horizon at recombination (see the first figure). For a
Universe devoid of spatial curvature (a flat or Euclidean geometry)
models predict
![]() . Thus, if the Universe were
flat, at an angular scale of precisely
. Thus, if the Universe were
flat, at an angular scale of precisely ![]() we would expect to
detect some characteristic feature in the CMB, the ``fingerprint'' of
recombination.
we would expect to
detect some characteristic feature in the CMB, the ``fingerprint'' of
recombination.
How can this feature be detected? One convenient way of comparing
theoretical model predictions with the result of observations is by
means of the functions ![]() , the CMB angular power spectrum of the
anisotropies. The microwave sky is expanded into a set of functions
labeled by the multipole index
, the CMB angular power spectrum of the
anisotropies. The microwave sky is expanded into a set of functions
labeled by the multipole index ![]() . The correspondence is such
that the
. The correspondence is such
that the ![]() th multipole samples angular scales of order
th multipole samples angular scales of order
![]() . Hence,
. Hence, ![]() gives us the typical
strength of the temperature perturbations on that angular scale. A
characteristic feature is given by the presence of peaks in the
gives us the typical
strength of the temperature perturbations on that angular scale. A
characteristic feature is given by the presence of peaks in the
![]() versus
versus ![]() plot. The first acoustic peak is
located at the multipole corresponding to the scale of the sound
horizon at recombination, when the plasma underwent its first
oscillation; it corresponds to a compression mode of the oscillating
plasma.
plot. The first acoustic peak is
located at the multipole corresponding to the scale of the sound
horizon at recombination, when the plasma underwent its first
oscillation; it corresponds to a compression mode of the oscillating
plasma.
Last year, the BOOMERanG collaboration announced results from
the Antarctic long duration balloon flight mission of 1998 (B98). They
found the first peak located at ![]() , at the right position
for a flat Universe [3,4]. Only weeks later, the results from
another balloon experiment, MAXIMA, were made available on the
internet [5,6]. MAXIMA produced high-resolution maps of a 100
square-degree patch of the northern sky and went beyond B98 in
exploring multipoles from
, at the right position
for a flat Universe [3,4]. Only weeks later, the results from
another balloon experiment, MAXIMA, were made available on the
internet [5,6]. MAXIMA produced high-resolution maps of a 100
square-degree patch of the northern sky and went beyond B98 in
exploring multipoles from ![]() to 785, the largest range
reported to date with a single experiment.
to 785, the largest range
reported to date with a single experiment.
Recently, a joint analysis of the COBE/DMR [7], B98 and MAXIMA
data sets was published [8]. The COBE data provide information
at low ![]() , necessary for normalization purposes. After correcting
for calibration uncertainties, the B98 and MAXIMA data were quite
consistent. The experiments used different observation strategies
and produced independent power spectra from regions of the sky roughly
, necessary for normalization purposes. After correcting
for calibration uncertainties, the B98 and MAXIMA data were quite
consistent. The experiments used different observation strategies
and produced independent power spectra from regions of the sky roughly
![]() apart and on opposite sides of the galactic plane. Their
consistency gives confidence in the results (see the second figure).
apart and on opposite sides of the galactic plane. Their
consistency gives confidence in the results (see the second figure).
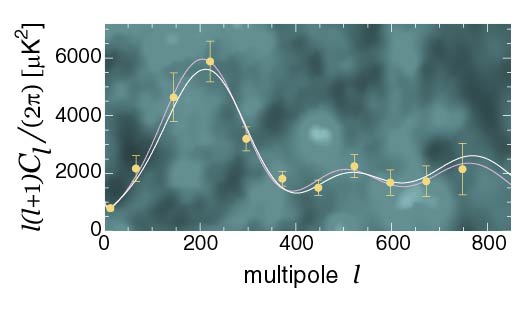 |
The presence of a localized and narrow (
![]() ) peak
at
) peak
at ![]() is in agreement with a flat Universe and favors an
inflationary model with initial adiabatic perturbations (where
fluctuations in each species are correlated). In the absence of a
possible later period of reionization, which could erase partly or even
completely the acoustic peaks, the physics of recombination predicts
the existence of other peaks; the second one corresponds to a
rarefaction mode and its characteristic scale is half that of the
first peak.
In the actual data we can see that following the first peak there is a
hint of a second one at
is in agreement with a flat Universe and favors an
inflationary model with initial adiabatic perturbations (where
fluctuations in each species are correlated). In the absence of a
possible later period of reionization, which could erase partly or even
completely the acoustic peaks, the physics of recombination predicts
the existence of other peaks; the second one corresponds to a
rarefaction mode and its characteristic scale is half that of the
first peak.
In the actual data we can see that following the first peak there is a
hint of a second one at ![]() , but nothing conclusive can be
said yet.
, but nothing conclusive can be
said yet.
Alternative models cannot reproduce these observations.
Cosmic topological defects in their simplest versions do not
predict the existence of this oscillation pattern. Topological
defects, such as cosmic strings and textures, which are concentrations
of primordial energy issued from early cosmological phase transitions,
can produce structure in the Universe, but cannot fit the present
data [9,10]. The complicated nonlinear evolution of the defect
network continuously perturbs the radiation background all along the
photon's journey in an incoherent fashion, leaving as its sole
characteristic signature a broad hump and virtually no acoustic
peaks [11]. Recent computer simulations with a cosmic
string model [12] have failed to generate the level of CMB
variations observed by B98 and MAXIMA on scales below ![]() .
.
The accurate locations and amplitudes of the expected secondary peaks
will allow the determination of many fundamental cosmological
parameters, such as a possible cosmological constant ![]() or
other forms of dark energy, such as
quintessence [13]. Full analysis of the B98 and
MAXIMA data sets will provide further insights, but conclusive results
will require inclusion of CMB polarization data [14] and full
sky coverage from the forthcoming satellite-based mission
MAP [15]. Other astrophysical input, such as supernovae and
large scale structure data, in combination with the CMB, has proven
very successful for removing degeneracies in the determination of
fundamental parameters and will be even more important in the
future.
or
other forms of dark energy, such as
quintessence [13]. Full analysis of the B98 and
MAXIMA data sets will provide further insights, but conclusive results
will require inclusion of CMB polarization data [14] and full
sky coverage from the forthcoming satellite-based mission
MAP [15]. Other astrophysical input, such as supernovae and
large scale structure data, in combination with the CMB, has proven
very successful for removing degeneracies in the determination of
fundamental parameters and will be even more important in the
future.
The increasing precision of today's detectors demands theoretical modeling to be highly accurate. The CMB contains a wealth of information on cosmology, and future experiments will test our models of structure formation to the limit.
References and Notes
- D. Scott et al., Science 268, 829 (1995) [ADS].
- S. Weinberg, preprint available at arXiv.org/abs/astro-ph/0006276.
- P. de Bernardis et al., Nature 404, 955 (2000) [ADS].
- C. Seife, Science 288, 595 (2000).
- A. Balbi et al., Astrophys. J. 545, L1 (2000) [ADS].
- S. Hanany et al., Astrophys. J. 545, L5 (2000) [ADS].
- C. Bennett et al., Astrophys. J. 464, L1 (1996) [ADS].
- A. Jaffe et al., Phys. Rev. Lett., in press.
- R. Durrer, A. Gangui, M. Sakellariadou, Phys. Rev. Lett. 76, 579 (1996) [APS]; preprint available at arXiv.org/abs/astro-ph/astro-ph/9507035.
- U.-L. Pen, U. Seljak, N. Turok, Phys. Rev. Lett. 79, 1611 (1997) [APS].
- J. Magueijo et al., Phys. Rev. Lett. 76, 2617 (1996) [APS].
- L. Pogosian, preprint available at arXiv.org/abs/astro-ph/0009307
- N. Bahcall et al., Science 284, 1481 (1999).
- M. Hedman et al., Astrophys. J., in press.
- See the Microwave Anisotropy Probe home page at map.gsfc.nasa.gov.
- The author is supported by Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) and the University of Buenos Aires (Argentina).
Some citing www pages:
* Research Preprint Highlights - February 2001 : Astrophysics (14 chosen from 506 preprints) .
* The Net Advance of Physics: INFLATION (Cosmology) . Or here .
* [sprechen Sie deutsch? - read the news on the Sternwarte Neumarkt then...] - [also here, in Astronomie-News] .

back to IAFE home page |
Back |

back to GRQTG home page |
The URL of this page is http://www.iafe.uba.ar/relatividad/gangui/maxima_science/ .
Edited by Alejandro Gangui