Superconducting Cosmic Strings
On a cold day, ice forms quickly on the surface of a pond. But it does not grow as a smooth, featureless covering. Instead, the water begins to freeze in many places independently, and the growing plates of ice join up in random fashion, leaving zig-zag boundaries between them. These irregular margins are an example of what physicists call "topological defects"-defects because they are places where the crystal structure of the ice is disrupted, and topological because an accurate description of them involves ideas of symmetry embodied in topology, the branch of mathematics that focuses on the study of continuous surfaces.
Current theories of particle physics likewise predict that a variety of topological defects would almost certainly have formed during the early evolution of the universe. Just as water turns to ice (a phase transition) when the temperature drops, so the interactions between elementary particles run through distinct phases as the typical energy of those particles falls with the expansion of the universe. When conditions favor the appearance of a new phase, it generally crops up in many places at the same time, and when separate regions of the new phase run into each other, topological defects are the result. The detection of such structures in the modern universe would provide precious information on events in the earliest instants after the Big Bang. Their absence, on the other hand, would force a major revision of current physical theories.
Cosmic topological defects lie at the intersection of particle physics, cosmology and condensed-matter physics. Laboratory experiments yield many examples of analogous phenomena-the water-to-ice transition being an elementary case-that can provide a bridge to understanding the very early universe. As cosmological theorists look for mechanisms that might have generated the features of the universe as we know it, few of their proposals can actually be modeled in the laboratory. Topological defects can. And among these, the most thoroughly studied are the phenomena called cosmic strings.
As imagined by physicists, cosmic strings are exceedingly narrow filaments of primordial material, strands of a trapped, unconverted phase left over from the early moments of cosmic history. They have extraordinary energies, move at velocities approaching that of light and curve space around themselves. Through their gravitational interactions they can draw matter together to form large-scale structures such as galaxies or clusters of galaxies, and push matter around to give such structures bulk drift velocities.
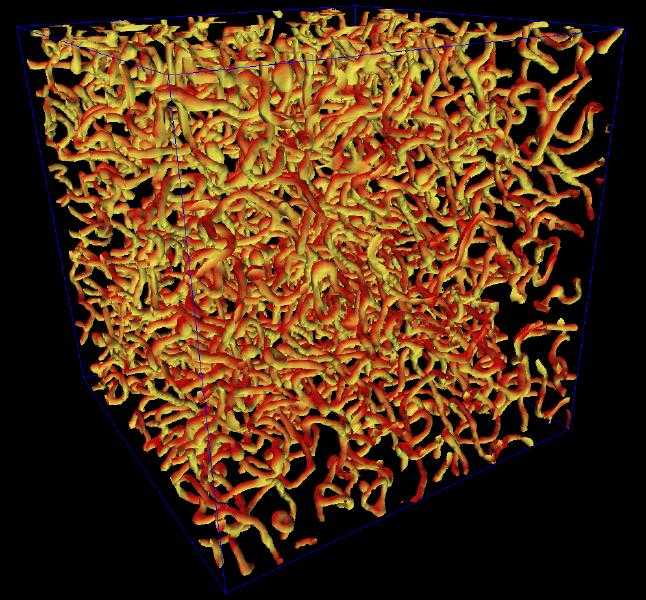
Cosmic strings can bend light rays from distant sources such as galaxies and quasars, and they can perturb the cosmic background radiation (or CMB, the so-called microwave background) in two ways. Around a hundred thousand years after the Big Bang, when this radiation broke free of its interaction with matter, a network of cosmic strings would have left its imprint on the background in the form of tiny temperature variations; since then, strings would continue to disturb the trajectories of free-streaming photons, adding further variations to their observed pattern today. In addition, the rapid movements and interactions of strings would produce a tangled network of long strings and loops (Figure 1) whose eventual decay would fill the universe with a background of gravitational waves.
Moreover, realistic particle-physics models predict that at a certain stage of their evolution these strings can develop tremendous electric currents, effectively becoming electrically conducting-actually superconducting-wires of astrophysical dimensions. This notion could help to explain some puzzles of observational cosmology. The currents would generate primordial magnetic fields that could give rise to the observed magnetic fields in galaxies today. Currents would also stabilize small loops of cosmic string against decay; such loops might still survive, forming so-called non-baryonic dark matter-the as-yet-undetected matter thought to occupy much of the modern universe.

Figure 1. When a body of water freezes over, ice begins forming in many places independently. As the frozen areas grow, they create irregular boundaries between areas of crystalline ice that have different orientations. Phase transitions in the early universe can likewise create topological defects, as regions of space where the transition has proceeded independently run up against each other. The author discusses the possibility that today's universe may, as a result, be riddled with high-energy, gravitationally powerful filaments of primordial material called cosmic strings. Above, a simulation shows a step in the evolution of one region of the universe, in which cosmic strings form from a random initial distribution of phases of a hypothetical field called a Higgs field. (Image above courtesy of Paul Shellard, Cambridge University.)
How Defects Form
Having built a model of elementary particles and forces, particle physicists and cosmologists are today embarked on a difficult search for a so-called Theory of Everything-a theory that unifies all the fundamental interactions. An essential ingredient in all major candidate theories is the concept of symmetry breaking. Experiments have determined that there are four physical forces in nature; in addition to gravity these are called the strong, weak and electromagnetic forces. At the very instant of the Big Bang, when energies were at their highest, it is believed that these forces were unified in a single, all-encompassing interaction. As the universe expanded and cooled down, first the gravitational interaction, then the strong interaction, and lastly the weak and the electromagnetic forces would have broken out of the unified scheme and adopted their present distinct identities in a series of symmetry breakings.
Theoretical physicists are still struggling to understand how gravity can be united with the other interactions, but for the unification of the strong, weak and electromagnetic forces plausible theories exist. Indeed, force-carrying particles whose existence demonstrated the fundamental unification of the weak and electromagnetic forces into a primordial "electroweak" force-the W and Z bosons-were discovered at CERN, the European accelerator laboratory, in 1983. (Note that particle physicists talk about two kinds of particles: fermions, which make up matter, and bosons, which are the quantized embodiments of particle forces and interactions.) In the context of the standard Big Bang theory, cosmological phase transitions are produced by the spontaneous breaking of a fundamental symmetry, such as the electroweak force, as the universe cools. For example, the electroweak interaction broke into the separate weak and electromagnetic forces when the universe was 10-12 seconds old, had a temperature of 1015 degrees Kelvin, and was only one part in 1015 of its present size. There are also other phase transitions besides those associated with the emergence of the distinct forces. The quark-hadron confinement transition, for example, took place when the universe was about a microsecond old. Before this transition, quarks-the particles that would become the constituents of the atomic nucleus-moved as free particles; afterward, they became forever bound up in protons, neutrons, mesons and other composite particles. All these phase transitions have exciting cosmological consequences and provide an important link between particle physics and cosmology.
The standard mechanism for breaking a symmetry involves a hypothetical field (loosely analogous to a magnetic or electrical field) called the Higgs field, named for Peter Higgs of the University of Edinburgh and pervading all space. As the universe cools, the Higgs field can adopt different ground states, also referred to as different vacuum states of the theory. In a symmetric ground state, the Higgs field is zero everywhere. Symmetry breaks when the Higgs field takes on a finite value. By suitably linking the Higgs field to other fields, the theoretical physicist can arrange that the transition from one vacuum state to another can induce a loss of symmetry among other interactions in a theory.

At a dinner table with full place settings, symmetry remains unbroken as long as the diners have not picked up any utensils. If all diners choose a wine glass to their right, the uniformity around the table will not be altered. If, however, one person chooses the wine glass at the left while another opts for the one on the right, and adjacent diners try to follow suit, `topological defects' will necessarily arise. One person will be left with two wine glasses, and another will have none. Like other comedies of its day, The Lady Eve (1941) derived its comic edge from romantic asymmetries between the herpetologically inclined Henry Fonda and the manipulative Barbara Stanwyck. (Image © and courtesy of Photo-fest.)
In 1976 Thomas Kibble of Imperial College, London first saw the possibility of defect formation when he realized that in a cooling universe, such a phase transition would not necessarily proceed in an orderly fashion. Rather, there would appear uncorrelated domains-separate regions in which the Higgs field adopts different values-because places sufficiently far apart would not have had enough time to "communicate" among themselves. The Higgs field in one region would have no way of knowing what the Higgs field in another is doing. As these regions began to merge, Kibble pointed out, it would not always be possible for the Higgs field to be in the same vacuum state everywhere.
The nature of the defects that form depends on the symmetries of the Higgs field itself. For example, the Higgs field may have a choice of two possible states to fall into. In this case, when regions that have taken opposite choices run up against each other, the boundary is marked by a structure called a domain wall, in which the Higgs field is obliged to pass through zero, creating a localized region where the vacuum state is one of unbroken symmetry (Figure 2).The domain wall is a microscopicallynarrow region trapping what physicists call a false vacuum, as distinct from the true vacuum on either side. The false vacuum ought not to exist, but does so because the geometry of the Higgs field does not allow it to disperse.
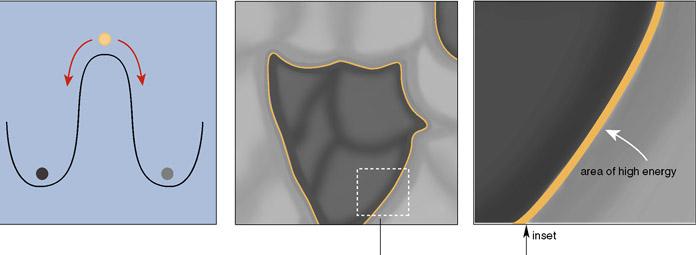
Figure 2. In a simple model of symmetry breaking, the initial symmetric ground state of the Higgs field (yellow dot) can fall into the left- or right-hand valley of an energy potential (light and dark dots), just as a diner can choose a wine glass from either the left or the right side. In a cosmic phase transition, regions of the new phase appear randomly and begin to grow and eventually merge as the transition proceeds toward completion (b). Regions in which the symmetry has broken the same way can coalesce, but where regions that have made opposite choices encounter each other, a topological defect known as a domain wall forms (c). Across the wall, the Higgs field has to go from one of the valleys in part (a) to the other, and must therefore traverse the energy peak. This creates a narrow planar region of very high energy, in which the symmetry is locally unbroken.
Domain walls are not a good thing for cosmology: They are huge, massive and hard to get rid of. Fortunately, a more likely and perhaps even beneficial possibility is a Higgs field with circular symmetry, meaning that its ground-state value can be represented by a point on the circumference of a circle. When domains of broken symmetry form, the choice the Higgs field makes in each one can be marked by an arrow pointing in any direction from 0 to 360 degrees. In this case, when mismatched domains come together, the Higgs field adjusts so as to concentrate the discontinuity into a line rather than a wall (Figure 3). This is a string defect, an incredibly thin filament of false vacuum. So-called Grand Unified Theories, which aim to unite the strong interaction with the already unified electroweak force, tend to contain Higgs fields that produce these cosmic strings.
More complex Higgs symmetries can give rise to defects known as monopoles and "textures." In all simple cases, the interiors of defects preserve the state of unbroken symmetry-the false vacuum-that prevailed before the transition occurred. These tightly confined regions would store incredible amounts of energy under conditions which are impossible to reproduce even in today's biggest particle accelerators. Needless to say this feature has attracted the interest of many cosmologists and particle physicists.

Figure 3. Symmetry breaking in a Higgs field with circular symmetry can be represented by a "Mexican hat" analogy. Because the Higgs ground state can lie anywhere within a circular valley in the field space, its position can be denoted by an arrow, like a compass needle, with an orientation from 0 to 360 degrees. (This direction denotes an internal orientation of the Higgs ground state, not a direction in physical space.) In a cosmic phase transition dictated by such a potential, arrows indicate the orientation of the Higgs field at different points in space. As separate regions of broken symmetry merge, it is not always possible for the field orientations to match. A cosmic string forms when, for purely topological reasons, the orientation of the arrows cannot be adjusted so as to keep the Higgs field in the minimum energy state at all places. At some distance from the string, the Higgs field sits in the broken symmetry state, but in the core of the string, it has to pass over the central peak of the Mexican hat, creating a narrow, extremely massive structure with unbroken symmetry along its axis.
Cosmology in the Laboratory
As I mentioned earlier, unlike any other proposed mechanism for the generation of observable cosmological features, topological defects can be reproduced in the laboratory! In fact, when all relevant lengths are uniformly scaled down, experimentalists have within reach a manageable laboratory experiment that offers a physical equivalent of the early universe. In 1985, Wojciech Zurek of the Los Alamos National Laboratory proposed testing the Kibble mechanism using the transition that the liquefied noble gas helium-4 makes from its normal state to the superfluid state, which exists at temperatures lower than about 2 degrees above absolute zero and in which fluid flow occurs without any friction.
If liquid helium were rapidly pressure- quenched around the critical temperature, Zurek argued, the rotation of the fluid as a whole would become trapped in a number of isolated vortices-tiny tornadoes, in effect. The vortices, carrying rotation in quantized amounts, would represent defects closely analogous to cosmic strings, and studying their formation might offer interesting hints for cosmology. Of course, although defects in condensed matter systems are topologically identical to those in field theory, there are also some important differences. The dynamics of the laboratory system is nonrelativistic, and friction is the controlling force, whereas in the cosmological case defects can move at almost the speed of light, and gravity is important. An additional technical difficulty is that the infinite and homogeneous nature of the universe before a phase transition cannot be matched by a laboratory sample of finite size.
Dealing with the superfluid transition of helium turned out to be hard, requiring extreme laboratory conditions. Some groups have demonstrated vortex generation, but it remains unclear how well the experimental findings match the Kibble-Zurek predictions. However, a more tractable laboratory analogue has been found, in the form of organic compounds called liquid crystals. In the second half of the 19th century chemists found several materials that behaved strangely around their melting point. In 1850, W. Heintz reported on the peculiarities of stearin, an organic compound used to waterproof paper and make metal polishes and soap. Heated from about 52 to 62 degrees Celsius, stearin first changed from a solid to a cloudy liquid, then took on an opaque coloring, then finally became a clear liquid. Similar behavior was later observed in other biological materials, leading eventually to the recognition of liquid crystals as a new form of matter-which got their badge of honor with the award of the 1991 Nobel Prize in Physics to Pierre-Gilles de Gennes for his accomplishments on order phenomena in liquid-crystal systems.
Liquid crystals are organic compounds with phases intermediate to the liquid and solid phases: They can flow like liquids while retaining anisotropic properties of crystalline solids, meaning that their molecular structure has a spatial alignment or orientation. They can be imagined as crystals whose molecules are able to move around, as in a liquid, while maintaining their relative orientation. For example, nematic liquid crystals consist of rodlike molecules, about 20 angstroms long, which tend to maintain themselves in a parallel alignment. Their structure endows them with useful optical properties. Such materials are used in digital displays, where electrical signals flip the orientation of the crystals, switching them between opaque and reflective states.
Liquid-crystal transitions occur at temperatures ranging from 10 to 200 degrees Celsius and generate structures easily detectable with the naked eye or with a microscope. These transitions proceed by the formation of domains, as different regions within a crystal settle into different alignments, so once again there is the possibility of defect formation. Experiments have shown that networks of defects in nematic crystals evolve in a self-similar manner, meaning that although the characteristic scale of the pattern changes, its maintains the same overall appearance. Such behavior is needed in a cosmological context for strings to be useful as progenitors of structure: Self-similarity means that the defects contribute a constant fraction of the universe's total energy density from small to large length scales.
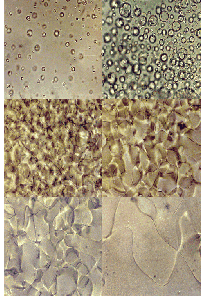
Figure 4. Cosmological-defect formation can be simulated in the laboratory by observing the transformation of liquid crystal between phases with different optical properties. In this sequence, bubbles of a new phase nucleate in an initially uniform liquid. As the bubbles grow and coalesce, their boundaries develop into structures analogous to cosmic strings. The scale of the pattern grows similarly to the way the scale of a network of cosmic strings increases with cosmic expansion. (Images courtesy of Ajit Srivastava, Institute of Physics, Bhubaneswar, India.)
Recently many groups have succeeded in carrying out a variation of Zurek's original idea using the superfluid transition in another isotope, helium-3, at temperatures close to 1 millikelvin, rather than the higher- temperature transition in helium-4. The discovery of superfluidity in helium-3 was recognized (a quarter of a century afterward) with the 1996 Nobel Prize in Physics awarded to David Lee, Douglas Osheroff and Robert Richardson. In 1996, Ville Ruutu and collaborators in Helsinki succeeded in heating up a volume of superfluid helium-3 with thermal neutrons to just above the transition temperature, then cooling it back through the superfluid transition. They observed copious production of quantized vortices. The precision in these experiments is such that the number of vortex lines can be monitored, allowing quantitative testing of defect-formation theories. Laboratory tests using both liquid crystals and helium have provided a kind of experimental confirmation of cosmological topological defect theory, increasing the credibility of these ideas. More advanced experiments with helium-3 have even probed the internal microscopic structure of the vortices, which forms a close analogy to cosmic strings whose internal structure allows the motion of particles, and thus electric currents, along them. As William Blake suggested, it is quite possible "to see a world in a grain of sand."
Gravitational Effects
If cosmic strings indeed formed about 10-35 seconds into the Big Bang, when the strong and electroweak forces went their separate ways, how would we look for them in the universe today? The cores of these strings are tiny indeed, no more than about 10-30 centimeter across, but their mass reaches incredibly high values, on the order of 10 million billion tons per centimeter. For comparison, recall that neutron stars are among the densest compact objects we know of. These are objects with approximately the mass of our sun, but with a radius of only 10 kilometers: their mass density is thus around 109 tons per cubic centimeter. Even if we squeezed one billion neutron stars into the size of an electron, we would still hardly reach the matter-energy density characteristic of grand unified cosmic strings!
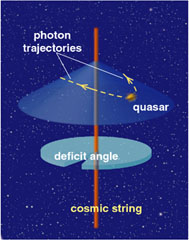
Massive objects exert gravitational pull, so such strings would betray their presence by their gravitational influence, in particular through the phenomenon of gravitational lensing, by which massive objects reveal themselves by bending the trajectories of photons, or quanta of light. Gravitational lensing serves nowadays as a useful observational tool for diagnosing the distribution of both luminous and dark matter in the universe. Consider first the highly idealized case of a stationary and perfectly straight string. According to Einstein's general theory of relativity, the presence of mass or energy curves spacetime, and this curvature in turn influences the trajectories of light and particles. Our straight string has a particularly simple effect on spacetime. Imagine a flat slice of space perpendicular to the string, cut a narrow wedge out of it, then glue the edges of the cut together (Figure 5). The resulting spatial section remains flat at all points but now has the topology of a cone. For a grand unified string, the size of the missing wedge-called the deficit angle-is tiny, no more than a few arcseconds.
Because space remains flat, an observer passing by the string will not feel any gravitational attraction toward it. An observer who travels around the string will, however, see the distant stars repeat themselves after a circuit that is less than a full 360-degree rotation by the amount of the deficit angle. The paths of all sorts of particles, whether photons, atoms or interstellar dust, will be deflected by approximately the deficit angle if they pass close by the string. This peculiar effect provides one detection method: A segment of string passing between us and a distant source, such as a quasar, will cause a splitting of the light rays and the formation of a double image. The separation of the two images is independent of how closely the light rays graze the string, and there is no magnification. These two features make lensing by a string distinguishable from lensing by a massive object such as a black hole, a neutron star or even a galaxy. In those cases, both the splitting of the images and their relative intensity depends on how closely light rays pass by the lensing object.
 |
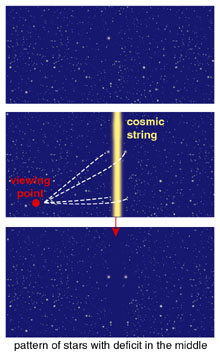 |
Figure 5. Cosmic strings affect surrounding spacetime by removing a small angular segment, creating a conelike geometry (above). Space remains flat everywhere, but a circular path around the string encompasses slightly less than 360 degrees. The deficit angle is tiny, about 10-5 radian. To an observer, the presence of a cosmic string would be betrayed by its effect on the trajectory of passing light rays, which are deflected by an amount equal to the deficit angle. The resultant gravitational lensing reveals itself in the doubling of images of objects behind the string (bottom panel, right). |
By deflecting the trajectory of ordinary matter rather than light, strings offer an interesting means of forming large-scale structure. A string sweeping through a distribution of interstellar dust will draw particles together in its wake, giving them lateral velocities of a few kilometers per second. The trail of the moving string will become a planar region of high-density matter, which, after gravitational collapse, could turn into thin, sheetlike distributions of galaxies, whose existence current observational surveys tend to indicate.
Although real strings would not in general be straight, they can be pictured as chains of small straight segments, to which the previous considerations will apply. A more significant complication is the existence of microscopic structure, in the form of irregular undulations which make strings effectively wiggly. These wiggles offer additional ways for cosmic strings to produce structure; because they represent local concentrations of energy, they act as sources of gravity in the conventional way. Wiggly strings can then produce not only planar structure distributions in their wakes, but also cosmologically long filaments, created by gravitational condensation along the string's length.
Although topological defects may be able to produce structure in the universe, it is not obvious that they can generate the right kind of structure. Cosmologists characterize the overall distribution of galaxies and clusters of galaxies by means of its power spectrum, which measures the magnitude of density variations as a function of length scale. Recent computer simulations, carried out by groups headed by Ruth Durrer of Geneva University and Neil Turok of Cambridge University, have suggested that defects would in general produce too little structure on large scales, corresponding to galaxy clusters or even bigger features. An additional test comes from the existence of tiny temperature variations in the cosmic microwave background. Density fluctuations that give rise to galaxies must also leave an imprint on the CMB, and these irregularities were finally detected by the COBE satellite in 1992. The simulations by Durrer and Turok failed to generate the observed level of CMB variations on an angular scale of one degree, which corresponds to the size of the observable universe about 300,000 years after the Big Bang, when the microwave background radiation last scattered from matter.
However, Paul Shellard's group, also at Cambridge, has tracked the evolution of cosmic strings in particular with higher resolution. They find that the overall spectrum of density fluctuations induced by strings has both an amplitude and a shape that are consistent, within observational uncertainties, with the latest data from galaxy surveys.
A recent analysis by Carlo R. Contaldi and João Magueijo of Imperial College, London and Mark Hindmarsh of the University of Sussex assumes that the CMB irregularities are the combined result of quantum fluctuations from an early period of cosmological inflation (exponential expansion driven by a vacuum energy associated with a Higgs field) along with perturbations seeded by cosmic strings generated at the end of inflation. Figure 6 compares the available observational data on CMB fluctuations with this and other theoretical predictions. The big vertical error bars indicate that reliable observational input to this branch of cosmology is still in short supply. Clearly it is still too early to draw definite conclusions, but as future experiments improve the data, structure-formation models seeded by cosmic strings will be subject to more constraining tests.
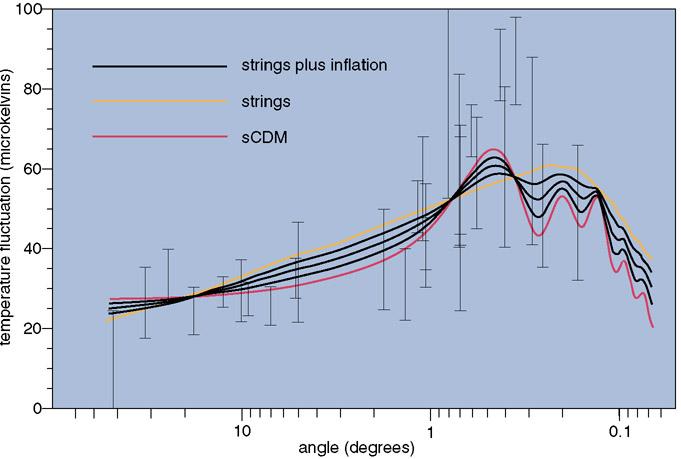
Figure 6. Tiny temperature variations detected in the cosmic microwave background (CMB) may result from some combination of quantum fluctuations during inflation of the universe and perturbations seeded by cosmic strings possibly produced at the end of inflation. The error bars above show the uncertainty ranges of observations of CMB fluctuations on different angular scales; the curves show that although strings alone do not fit well the degree-scale observations (yellow line), the predictions of the standard cold-dark-matter model (sCDM, red line) and three models incorporating cosmic strings (black lines) all lie within the range of CMB observations. (Adapted from Contaldi et al. 1999.)
Currents Along Strings
In the past few years it has become clear that topological defects, and in particular strings, will be endowed with a considerably richer structure than previously envisaged. In generic grand unified models, the Higgs field, responsible for the existence of cosmic strings, has interactions with other fundamental fields. This is no surprise, since in the better-understood electroweak theory, it is the interaction of a Higgs field with other fields that accounts for the observed masses of light fermions such as the familiar electron and the W and Z bosons. Inside the string, the Higgs field is trapped in its high-energy state, and if it is coupled to another fundamental field, that too will exhibit unusual behavior. If the other field is electromagnetically charged, for example, it may manifest itself as a current flowing along the string core.
The existence of such currents, whether electromagnetic or not, has a crucial effect on the dynamics of circular loops of string. A loop that carries no current has no defining feature that would allow any physical definition of rotation, but the existence of a current breaks the circular symmetry, marking a definite direction. This allows the loop configuration as a whole to rotate. Such currents also allow the existence of stable loops of fixed microscopic size, in which the angular momentum of the current balances string tension. These stationary-loop solutions were dubbed "vortons" by Richard L. Davis and Paul Shellard in 1988.
The behavior of a trapped charged field is such that current-carrying string is not just a conductor but a superconductor-current flows even without an electric field to drive it and without any dissipation. Moreover, vortons become quantized because the internal field has to match up on itself around the loop, and this means that current must flow in discrete quantities. Because the current can change only through quantum jumps, vortons do not radiate energy in a classical way, even though they are oscillating electromagnetic structures. At large distances these vortons look like point masses with quantized electric charge (actually they can have more than a hundred times the charge of the electron) and angular momentum. They are very much like particles, hence their name. They are however very peculiar, for their characteristic size is found by multiplying their charge number (around a hundred) by the string thickness, which is essentially some 14 orders of magnitude smaller than the classical electron radius. Also, having been created during symmetry breaking they must have a mass roughly equivalent (in mass-energy terms) to the energies of grand unification; therefore a vorton would be some 20 orders of magnitude heavier than the electron.
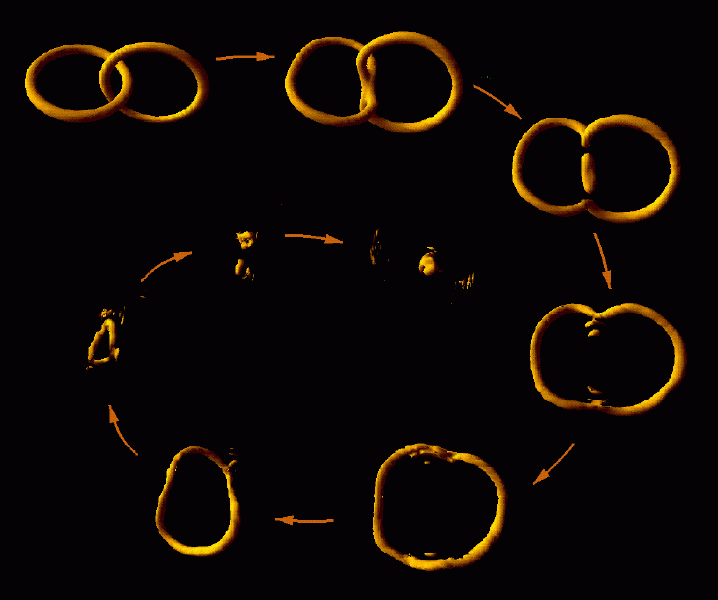
Figure 7. Loops of cosmic string can both merge and lose energy by the emission of (mainly gravitational) radiation, as in this simulation by Richard Battye and Paul Shellard. Shrinking loops can eventually disappear altogether, although if the string is of a type that carries a current, it is possible for the loop to stabilize at a certain size. The current in such a loop is quantized, preventing the slow radiative loss of energy. A large population of stabilized loops-called vortons-would be a problem for cosmology, since it would contribute an unacceptably large mass density to the universe.
The stability that currents give to loops of superconducting string potentially creates a big problem. Astronomical measurements have given us estimates of the amount of mass in the universe. Although some mass is not accounted for, these vortons would be extremely massive objects with an abundance that would probably not be compatible with standard cosmology. Their stability may not be absolute, however. In realistic models of particle physics, a subsequent phase transition, at a lower energy than the one that created the vortons, might disrupt the string currents and allow the vortons to decay.
Another way of getting rid of the excess of abundance of these objects-at least some of it-is to take account of electromagnetic self-interactions. The electromagnetic field in the vicinity of a conducting string will interact with the very same string current that generated it, modifying its energetic stability. In work done with Brandon Carter's group at the Observatoire de Paris-Meudon, we have found that these effects may significantly change the vorton distribution, diminishing their abundance to acceptable levels (Figure 8).
Finally, if strings formed at energies much lower than grand unification energies (close to the electroweak transition, for example), then vortons would be much less massive, and their abundance would cease to be a problem. In fact they could be useful in explaining both the missing dark matter of the universe as well as certain enigmatic cosmic rays of very high energy. Present estimates suggest that such low-energy vortons could comprise 6 percent of the critical density of the universe (the density required to make the universe eventually collapse back on itself rather than expand forever, in the absence of a cosmological constant or other nonstandard vacuum-energy term).
Conducting strings, like the nonconducting variety, can produce gravitational lensing, but they exert additional effects that give them a specific observational fingerprint. Pulses of current traveling along a string generate a local and transient gravitational curvature that could, for example, cause quasar images to describe peculiar, symmetric elliptical figures in the sky, during which the frequency of the quasar's emissions would also change in a predictable manner. Detection of this signature would not only show that strings exist, but would prove that they are of the conducting type.
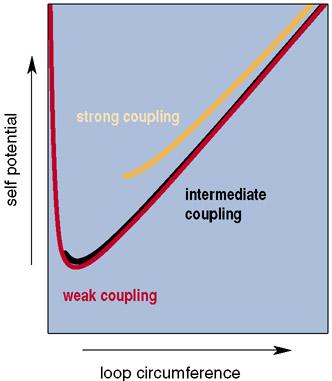
Figure 8. Whether a string loop can form a stable vorton depends on details of particle physics. The current in a loop generates a special dynamics, represented here by a self-interaction potential as a function of loop circumference (on an arbitrary scale). If the coupling of the string current to the electromagnetic field is weak, the potential has a minimum, allowing a stable loop to exist. If the coupling is strong, the loop shrinks to a size where particles can escape by quantum tunneling, and no stability is possible.
Astrophysical Footprints
Two outstanding astrophysical problems may perhaps be explained with the help of superconducting cosmic strings. The first concerns how galactic magnetic fields are generated. In the most commonly held scenario, the magnetic fields possessed by galaxies today arose from smaller seed fields that already existed before galaxies themselves formed. These seed fields would have only a small coherence length-the average size of a region with a roughly uniform field-but standard magnetohydrodynamic theory allows both the strength of the field and its coherence length to grow to galactic scales.
A field incorporated into a protogalactic structure remains trapped as that structure grows; in particular, as the protogalaxy shrinks under its own gravity, the magnetic flux within it is compressed too, increasing the strength (flux per unit area) of the field. Rotation of the evolving system may then increase the field strength further, through a dynamo effect, to the value typical of galactic magnetic fields, roughly 10-6 gauss. However, this scenario is not universally accepted, and other models are being studied that would produce tiny primordial fields that already have a large coherence length.
Superconducting cosmic strings may be able to do the job. They carry electric currents, and in fact fairly large ones. In 1985, Edward Witten of the Institute for Advanced Study in Princeton was the first to suggest that strings could become superconducting, and he calculated a maximum current based on the mass and charge of a string's current-carrying fermion. If one imagines an electron as the current carrier, this current reaches some tens of amperes, but for particles on the grand unified mass scale, currents more like 1020 amperes are expected-enormous even by astrophysical standards. Magnetic fields are produced when an electrically charged object moves in space; theoretically this is precisely what cosmic strings are and what they do. Calculations suggest that superconducting strings could generate interesting seed magnetic fields with strengths of about 10-20 gauss and with coherence scales of roughly 100 kiloparsecs. (One parsec equals 3.258 light-years.) This corresponds to the size of protogalaxies, and dynamo effects could then increase the field strength to the observed values. The string's motion through the turbulent primordial plasma might induce vorticity that could also amplify field strengths. Conducting strings could thus easily provide magnetic fields that would evolve into modern galactic fields.
The second problem is much closer to home. Earth's atmosphere is constantly assaulted by lots of particles, such as photons, electrons, protons and heavier nuclei. Recent detections have recorded astonishingly energetic cosmic-ray events, with energies on the order of a few hundred exaelectron-volts (1 Eev = 1018 electron-volts). This is roughly the kinetic energy of a tennis ball traveling at over 100 miles an hour, all concentrated into an atomic particle. Particles with such energies cannot easily move through intergalactic space, which, far from being empty, is pervaded by cosmic background radiation fields, including the microwave background as well as diffuse radio backgrounds. From the perspective of particles moving faster than some critical velocity, these fields look like bunches of very damaging photons, which degrade the particle's energy through collisions and scattering. For example, a proton that reaches Earth's atmosphere with the necessary energy to explain these ultra-energetic events could not have come from farther away than about 30 million parsecs, according to a result known as the Greisen-Zatsepin-Kuz'min (GZK) cutoff.
One might therefore conclude that the ultra-high-energy cosmic rays must come from sources that are close (astrophysically speaking) to our galaxy. However, unusual and energetic objects like quasars and active galactic nuclei are mostly too far away. The high-energy particles remain a mystery because when one looks back in the direction they came from, there is nothing nearby that could have given them the necessary kick! So what are they, and how did they manage to reach us?
For the time being, standard astrophysics seems unable to answer these questions, and in fact essentially states that we should not receive any such rays. As Ludwik Celnikier from the Observatoire de Paris-Meudon has said, comparing cosmological dark matter to ultra-high-energy cosmic rays: The former is a form of matter which should exist, but until further notice doesn't, whereas the high-energy rays are particles which do exist but perhaps shouldn't.
This is where topological defects, and in particular superconducting cosmic strings, can lend a hand. They offer two ways to deliver extremely energetic particles: They may directly emit particles with tremendous energies, or, more excitingly, they may send off tiny loops of superconducting cosmic string which would then be misinterpreted as ordinary but very energetic particles.
The first mechanism arises because the currents carried by strings can be thought of as streams of trapped particles, which would in general be extremely massive and unstable. Like neutrons, however, which decay in a few minutes when left by themselves but live happily inside nuclei, these heavy particles can exist indefinitely when confined within strings. Indeed, cosmic strings are the only objects that could preserve such particles from their origin to the present time. The trapped particles can nonetheless emerge occasionally when strings suffer violent events. A single string may bend sharply to create a kink or cusp, or a pair of strings may intersect in such a way that their ends switch partners. In these events some trapped particles can find their way out of the string, at which time they would almost instantly decay. They are so massive, however, that the light particles produced in their decay would be energetic enough to qualify as ultra-high-energy cosmic rays.
The second possibility comes from Silvano Bonazzola and Patrick Peter of the Observatoire de Paris-Meudon, who have recently proposed that the high-energy rays are in fact vortons. Because vortons typically have more than a hundred times the charge of an electron, they are efficiently accelerated along electric field lines in active galactic nuclei. Their huge mass, moreover, means that compared to protons they need smaller velocities to attain equivalently high energies, and these lower velocities mean they can travel enormous distances without running up against the GZK cutoff. A vorton hitting any air molecule in the atmosphere would decay as if it were a very energetic but otherwise ordinary particle. The interaction of the trapped current carriers in the vorton with the quarks within atmospheric protons would proceed with a characteristic energy spectrum (Figure 9), which would be mirrored by the energy spectrum of observed high-energy rays. It is hoped that the enigma of ultra-high-energy cosmic rays will be clarified in the near future with the construction in Argentina and the United States of components of the very large Pierre Auger Observatory, named after the French physicist who was the first to discover, on top of the French Alps in the late 1930s, the showers of secondary particles in the atmosphere triggered by cosmic rays. This array of detectors is planned for early next century and will observe so many of these high-energy events that it should be possible to deduce the ray's identity-and test whether cosmic strings are indeed the cause.
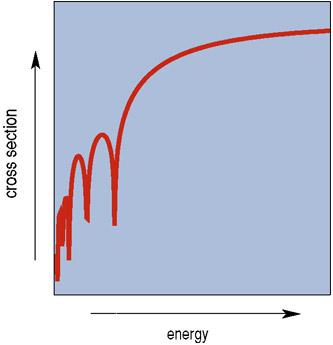
Figure 9. Interaction of a vorton with a proton in Earth's atmosphere varies with energy in a way that depends on the interaction of quarks inside the proton with current-carrying particle states in the string loop. Ultra-high-energy cosmic rays created in this way might have a characteristic energy spectrum that would identify vorton collisions as their origin.
It is both curious and important that fragments from the universe's birth may still be shaping the fate of galaxies. François, duc de La Rochefoucauld, had human frailty in mind when he wrote his Maximes. But he might just as well have been thinking of cosmic strings when he wrote: "Il y a de certains défauts qui, bien mis en oeuvre, brillent plus que la vertu même."
Bibliography
Brandenberger, R., B. Carter, A.-C. Davis and M. Trodden. 1996. Cosmic vortons and particle physics constraints. Physical Review D 54:6059-6071.
Bonazzola, S., and P. Peter. 1997. Can high energy cosmic rays be vortons? Astroparticle Physics 7:161-172.
Bowick, M., et al. 1994. The cosmological Kibble mechanism in the laboratory: String formation in liquid crystals. Science 236:943-945.
Carter, B., P. Peter and A. Gangui. 1997. Avoidance of collapse by circular current-carrying cosmic string loops. Physical Review D 55:4647-4662.
Chuang, I., et al. 1991. Cosmology in the laboratory: Defect dynamics in liquid crystals. Science 2351:1336-1342.
Contaldi, C., M. Hindmarsh and J. Magueijo. 1999. CMB and density fluctuations from strings plus inflation. Physical Review Letters 82:2034-2037.
Davis, R. L., and E. P. S. Shellard. 1988. The physics of vortex superconductivity. Physics Letters B 207:404-410.
de Gennes, P. G. 1974. The Physics of Liquid Crystals. Oxford, U.K.: Clarendon Press.
de Laix, A., L. M. Krauss and T. Vachaspati. 1999. Gravitational lensing signature of long cosmic strings. Physical Review Letters 79:1968-1971.
Durrer, R., A. Gangui and M. Sakellariadou. 1996. Doppler peaks in the angular power spectrum of the cosmic microwave background: A fingerprint of topological defects. Physical Review Letters 76:579-582.
Gangui, A., P. Peter and C. Boehm. 1998. Could electromagnetic corrections solve the vorton excess problem? Physical Review D 57:2580-2589.
Kibble, T. W. B. 1976. Topology of cosmic domains and strings. Journal of Physics A 9:1387-1398.
Kibble, T. W. B. 1980. Some implications of a cosmological phase transition. Physics Reports 67:183-289.
Martins., C. J. A. P., and E. P. S. Shellard. 1998. Galactic magnetic fields from superconducting strings. Physical Review D 57:5276-5279.
Pen, U.-L., U. Seljak and N. Turok. 1997. Power spectra in global defect theories of cosmic structure formation. Physical Review Letters 79:1611-1614.
Ruutu, V. M. H., et al. 1996. Vortex formation in neutron-irradiated superfluid 3He as an analogue of cosmological defect formation. Nature 382: 334-336.
Vilenkin, A., and E. P. S. Shellard. 1994. Cosmic Strings and Other Topological Defects. Cambridge, U.K.: Cambridge University Press.
Witten, E. 1985. Superconducting strings. Nuclear Physics B 249:557-592.
Wu, J. H. P., P. P. Avelino, E. P. S. Shellard and B. Allen. In press. Cosmic strings, loops, and linear growth of matter perturbations. Preprint astro-ph/9812156 at http:// xxx.lanl.gov.
Zurek, W. H. 1996. The shards of broken symmetry. Nature 382:296-298.
arXiv: astro-ph/0005186 8 May 2000 (enhanced version 20 Feb 2001)
Journal style (still without ©'ed figures) here. Also some Links.
* See also the News of Science coverage of this article by the weekly e-mail digest journal SCIENCE-WEEK (June 9, 2000 - Vol. 4 Number 23, news number 6.)
* People also found this useful as a Quantum Mechanics PROJECT, fall 2001 at Chalmers Goteborg University.
Thanks to all the people who generously provided figures and scientific input. Thanks also to `American Scientist' (and especially to Rosalind!) for permission to post my article here. -A.G.
 back to the Observatoire home page |
Back |
 back to DARC home page |
The URL of this page is http://cms.iafe.uba.ar/gangui/SCS.html .
Edited by Alejandro Gangui